|
||||||||||||||||
|
||||||||||||||||
|
|
|
|
MANDELBROT SET |
|
|
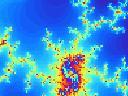
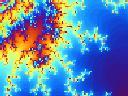
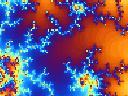
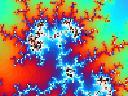
The Mandelbrot Set is a set of points which forming a fractal pattern named after Benoît Mandelbrot, who is its discoverer and who has made extensive studies of this set of points and fractals. The Mandelbrot Set is a set of points on the complex plane, whose definition is based on the simple iterative equation zn+1 = zn2 + c where c is a complex number. The Mandelbrot set is defined a the set of all c’s such that when substituted into the above iterative equation, the absolute value of z will be bounded after applying the above recursive equation repeatedly using any initial value for z. Although the Mandelbrot Set arises from a simple equation, when computed and plotted, the Mandelbrot Set forms a fractal complicated structure. Its shape and structure come with aesthetic appeal and many interesting properties under various scaling or magnifications. Various fractal images may be formed from the magnifications of Mandelbrot Set. Below are different parts of the Mandelbrot set under various magnifications:
|
|
|
Bits and Beyond... DESCARTES Ranè Descartes (1596-1650) was a 17th century French philosopher and mathematician. He received his education in mathematics, classics, and law at La Flèche and Poitiers. After a brief service in the military, he settled in Holland where he made significant contributions to the field of Algebra, Analytic Geometry, and Calculus. The commonly used Cartesian Coordinate System was named after him. His work, La géométrie, includes his contributions to algebra and geometry.
|